sin in C/C++: calculating sine

👋 Hey there! In this article, we’re diving into the sin function in C/C++. This function calculates the sine of an angle. We’ll start off by exploring how to use this function and then try implementing it ourselves. At the end of the article, you’ll find exercises further practice.

Похожее

The tan Function in C++: Understanding Angles and Ratios

C++ offers many ways to handle mathematical tasks. One of them is the tan function which deals with angles. This article will help you understand and use this function, see it in action, and even create your own simple program using tan.

How to calculate sine in C++

To calculate sine in C++, you can use the sin function. This function is declared in the <math.h> header file. For C++, you can include <cmath>. The function is structured as:

double sin (double x);

• The function takes a floating-point number as its argument, which represents the angle in radians.
• It returns the sine of the provided angle.

Let’s look at an example of how to use this function:

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  cout << "sin(M_PI * 1 / 2) = " << sin(M_PI * 1 / 2) << endl;
  cout << "sin(M_PI * 2 / 3) = " << sin(M_PI * 2 / 3) << endl;
  cout << "sin(M_PI) = " << sin(M_PI) << endl;
  cout << "sin(0) = " << sin(0) << endl;
  cout << "sin(2 * M_PI) = " << sin(2 * M_PI) << endl;

  return 0;
}

The constant M_PI becomes accessible after including the <cmath> header. This number is approximately 3.1415.

Program’s output:

sin(M_PI * 1 / 3) = 1
sin(M_PI * 2 / 3) = 0.866025
sin(M_PI) = 1.22465e-16
sin(0) = 0
sin(2 * M_PI) = -2.44929e-16

For the numbers M_PI and 2 * M_PI, we got values very close to zero, but not precisely. This is due to the finite precision of the M_PI constant, unlike π in mathematics.

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  cout << "sin(2*M_PI + M_PI / 2) = " << sin(2*M_PI + M_PI / 2) << endl;

  return 0;
}

Implementing sin on your own

To compute the sine without relying on external libraries, we can use the Taylor series. This series allows us to represent the sine as a summation:

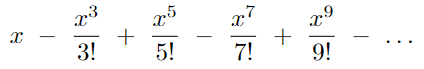
Let’s implement a function that computes this series:

#include <cmath>
#include <iostream>

using namespace std;

// In this function, we'll recursively calculate the factorial of a number
int factorial(int n) {
  if (n == 0) {
    return 1;
  }

  return n * factorial(n - 1);
}

// Calculation of a number's power
double pow(double base, int exponent) {
  double result = 1;
  for (int i = 0; i < exponent; i++) {
    result *= base;
  }

  return result;
}

// We need to know the sign of the number
double sign(double x) {
  if (x > 0) {
    return 1;
  } else if (x < 0) {
    return -1;
  } else {
    return 0;
  }
}

// Calculating sine using the above Taylor series
double my_sin(double x) {
  // Our implementation only works for numbers from -2*M_PI to 2*M_PI
  // Therefore, we use the fact that sin(x) == sin(x + 2*M_PI) for any x
  while (fabs(x) >= 2 * M_PI) {
    x -= sign(x) * 2 * M_PI;
  }

  double result = x;
  // Here we calculate 4 terms of the series
  // We can compute more terms for better precision
  for (int i = 1; i <= 4; i++) {
    double term = (double)pow(x, 1 + 2 * i) / factorial(1 + 2 * i);
    if (i % 2 == 1) {
      result -= term;
    } else {
      result += term;
    }
  }
  return result;
}

int main() {
  cout << "my_sin(M_PI * 1 / 2) = " << my_sin(M_PI * 1 / 2) << endl;
  cout << "my_sin(M_PI * 2 / 3) = " << my_sin(M_PI * 2 / 3) << endl;
  cout << "my_sin(M_PI) = " << my_sin(M_PI) << endl;
  cout << "my_sin(0) = " << my_sin(0) << endl;
  cout << "my_sin(2 * M_PI) = " << my_sin(2 * M_PI) << endl;
  return 0;
}

Output of this program:

my_sin(M_PI * 1 / 2) = 1
my_sin(M_PI * 2 / 3) = 0.866108
my_sin(M_PI) = 0.00692527
my_sin(0) = 0
my_sin(2 * M_PI) = 0

As you can see, our function computes the sine of an angle with some error. You can adjust number of terms in my_sin cycle for better precision.

sinl and sinf functions

The functions sinl and sinf work pretty much like the regular sin, just with different types. Let’s take a peek at the prototype of sinl:

long double sinl (long double x);

As you can see, the sinl function takes in and returns a long double (while sin just takes and returns a double). Now, let’s have a look at sinf:

float sinf (float x);

Here we see float. Now, let’s try to compare the results of these functions:

cout << "sinf(M_PI) = " << sinf(M_PI) << endl;
cout << "sin (M_PI) = " << sin(M_PI) << endl;
cout << "sinl(M_PI) = " << sinl(M_PI) << endl;

The program’s output:

sinf(M_PI) = -8.74228e-08
sin (M_PI) = 1.22465e-16
sinl(M_PI) = 1.22465e-16

All the results are close to zero, but they do vary slightly. This is because of the different precision of the data types they handle.

Похожее

sqrt in C/C++: calculating square root

Understand and implement the square root function in C and C++ with examples, differences between variants of the function, and exercises for reinforcement.

Exercises

1. Using sin:
   Write a C++ program that prompts the user for an angle in radians, calculates its sine using the sin function, and then displays the result. Also, the program should display the angle input by the user.

2. Your own sin implementation:
   Using the Taylor series from the article, craft your own sine function. Test its performance with different angles and compare the results with the standard sin function.

3. Comparing accuracy:
   Develop a program that compares the sine computation results using the standard sin function and your own implementation. Display the difference between them for various angles.