exp in C/C++: calculating the exponent

👋 Hi! This article will discuss the exp function, which calculates the exponent of a number in C/C++. We will start by using this function with an example, then try to implement it ourselves. We will also understand how exp is different from expl and expf. At the end of the article, there will be exercises for further practice.

Похожее

srand in C++: initializing the random number generator

The srand function is used in C++ for initializing the random number generator. This article will explore how to use this function with examples. At the end of the article, there are exercises for further.

Calculating the exponent of a number in C/C++

To calculate the exponent of a number in C/C++, the built-in exp function can be used. This function is accessible after including the <math.h> file. In C++, you can include <cmath>. Below is the prototype of this function:

double exp (double x);

• The function takes a single argument: the number for which the exponent needs to be calculated.
• The function returns the exponent of the argument passed to it.

Here is an example:

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  cout << "exp(1) = " << exp(1) << endl;
  cout << "exp(2) = " << exp(2) << endl;
  cout << "exp(10) = " << exp(10) << endl;
  cout << "exp(0) = " << exp(0) << endl;
  cout << "exp(0.25) = " << exp(0.25) << endl;
  cout << "exp(-2) = " << exp(-2) << endl;
  cout << "exp(-4.567) = " << exp(-4.567) << endl;

  return 0;
}

Program output:

exp(1) = 2.71828
exp(2) = 7.38906
exp(10) = 22026.5
exp(0) = 1
exp(0.25) = 1.28403
exp(-2) = 0.135335
exp(-4.567) = 0.0103891

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  double x = 2.5;
  cout << exp(x + 1) / exp(x) << endl;
  return 0;
}

Implementing exp yourself

To compute the exponent ourselves, the Taylor series can be used. The exponent expanded into a Taylor series looks like this:

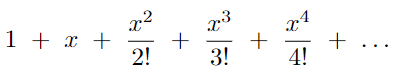
The program:

#include <cmath>
#include <iostream>

using namespace std;

// Function to compute the factorial of a number
double factorial(int n) {
  if (n == 0) return 1.0;
  double result = 1.0;
  for (int i = 1; i <= n; ++i) {
    result *= i;
  }
  return result;
}

// Function to compute e^x using the Taylor series
double my_exp(double x, int num_terms = 20) {
  double result = 1.0;  // Start with the first term of the Taylor series (1)

  for (int n = 1; n <= num_terms; ++n) {
    result += pow(x, n) / factorial(n);
  }

  return result;
}

int main() {
  cout << "my_exp(1) = " << my_exp(1) << endl;
  cout << "my_exp(2) = " << my_exp(2) << endl;
  cout << "my_exp(10) = " << my_exp(10) << endl;
  cout << "my_exp(0) = " << my_exp(0) << endl;
  cout << "my_exp(0.25) = " << my_exp(0.25) << endl;
  cout << "my_exp(-2) = " << my_exp(-2) << endl;
  cout << "my_exp(-4.567) = " << my_exp(-4.567) << endl;

  return 0;
}

Output:

my_exp(1) = 2.71828
my_exp(2) = 7.38906
my_exp(10) = 21991.5
my_exp(0) = 1
my_exp(0.25) = 1.28403
my_exp(-2) = 0.135335
my_exp(-4.567) = 0.0103902

In the program above, twenty iterations for exponent calculation are performed. The number of iterations can be changed to be larger or smaller by passing a second argument num_terms (default is twenty), depending on the accuracy needed.

Functions expl and expf

The functions expl and expf, like exp, compute the exponent of a number. The only difference is that they work with floating-point numbers of type long double (expl) and float (expf). Here is an example:

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  cout << "expl(234) = " << expl(234) << endl;
  cout << "exp (234) = " << exp(234) << endl;
  cout << "expf(234) = " << expf(234) << endl;

  return 0;
}

Output:

expl(234) = 4.21608e+101
exp (234) = 4.21608e+101
expf(234) = inf

As you can see, they return the same number, just of a different type. In the case of expf, the number overflowed, resulting in inf.

Похожее

string::size in C++: Measuring String Length

C++ offers a variety of tools to work with strings, and one of the most essential functions is string::size. In this article, we'll dive deep into this function, understand how it measures strings, and explore its real-world applications.

Exercises

1. Using exp, expl, and expf:
   Write a C++ program that prompts the user for a number and the type of the number (double, long double, float), then computes the exponent of this number using the corresponding function (exp, expl, expf) and displays the result. Also, display the original number entered by the user.

2. Comparing exp and my_exp:
   Using the example provided in the article, compare the results of the standard exp function and your version of the my_exp function for different numbers. Write a program that demonstrates the differences in the results and displays them on the screen.

3. Using expf with large numbers:
   Write a program that demonstrates overflow when using the expf function with large numbers. Your program should use the exp, expl, and expf functions, and the results of their work should be displayed on the screen.