cos в C/C++: разбираемся с примерами

👋 Привет! В этой статье мы разберем функцию cos в C/C++. Эта функция вычисляет косинус угла. Начнем мы с рассмотрения примера использования этой функции, а потом попробуем реализовать ее самостоятельно. В конце статьи вы найдете упражнения для закрепления материала.

Иллюстрация косинуса
Интересное
Последние новости в мире программирования
Самые свежие новости и полезные материалы в моем telegram канале.
go

Как вычислить косинус в C++

Для вычисления косинуса в C++ мы можем воспользоваться функцией cos. Эта функция объявлена в заголовочном файле math.h. В C++ вы можете подключать cmath. Выглядит эта функция следующим образом:

double cos (double x);
  • Первым аргументом функция принимает вещественное число. Тут мы передаем угол в радианах, для которого нужно посчитать косинус.
  • Функция возвращает косинус переданного ей угла.

Давайте посмотрим на пример использования этой функции:

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  cout << "cos(M_PI * 1 / 3) = " << cos(M_PI * 1 / 3) << endl;
  cout << "cos(M_PI * 2 / 3) = " << cos(M_PI * 2 / 3) << endl;
  cout << "cos(M_PI) = " << cos(M_PI) << endl;
  cout << "cos(0) = " << cos(0) << endl;
  cout << "cos(2 * M_PI) = " << cos(2 * M_PI) << endl;

  return 0;
}

Константа M_PI доступна после подключения библиотеки <cmath>. Это число примерно равно 3.1415.

Вывод программы:

cos(M_PI * 1 / 3) = 0.5
cos(M_PI * 2 / 3) = -0.5
cos(M_PI) = -1
cos(0) = 1
cos(2 * M_PI) = 1

Что будет выведено на экран?

#include <cmath>
#include <iostream>

using namespace std;

int main() {
  cout << "cos(M_PI / 4) = " << cos(M_PI / 4) << endl;

  return 0;
}
0.5
0.7071
-0.5
-0.7071

Как реализовать cos самому

Для вычисления косинуса без помощи сторонних библиотек, мы воспользуемся рядом Тейлора. Он позволяют разложить косинус на сумму вида:

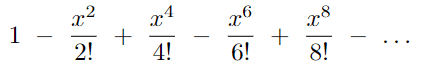
Ряд Тейлора для cos

Давайте реализуем функцию, которая будет подсчитывать этот ряд:

#include <cmath>
#include <iostream>

using namespace std;

// в этой функции мы будем считать факториал числа рекурсивно
int factorial(int n) {
  if (n == 0) {
    return 1;
  }

  return n * factorial(n - 1);
}

// подсчет степени числа
double pow(double base, int exponent) {
  double result = 1;
  for (int i = 0; i < exponent; i++) {
    result *= base;
  }

  return result;
}

// нам нужно будет знать знак числа
double sign(double x) {
  if (x > 0) {
    return 1;
  } else if (x < 0) {
    return -1;
  } else {
    return 0;
  }
}

// подсчет косинуса через ряд Тейлора выше
double my_cos(double x) {
  // наша реализация работает только для чисел от -2*M_PI до 2*M_PI
  // поэтому мы пользуемся тем, что cos(x) == cos(x + 2*M_PI) для любого x
  while (fabs(x) >= 2 * M_PI) {
    x -= sign(x) * 2 * M_PI;
  }

  double result = 1;
  // тут мы подсчитываем 4 элементов ряда
  // можно подсчитывать больше для лучшей точности
  for (int i = 1; i <= 4; i++) {
    double term = (double)pow(x, 2 * i) / factorial(2 * i);
    if (i % 2 == 1) {
      result -= term;
    } else {
      result += term;
    }
  }
  return result;
}

int main() {
  cout << "my_cos(M_PI * 1 / 3) = " << my_cos(M_PI * 1 / 3) << endl;
  cout << "my_cos(M_PI * 2 / 3) = " << my_cos(M_PI * 2 / 3) << endl;
  cout << "my_cos(M_PI) = " << my_cos(M_PI) << endl;
  cout << "my_cos(0) = " << my_cos(0) << endl;
  cout << "my_cos(2 * M_PI) = " << my_cos(2 * M_PI) << endl;
  return 0;
}

Вывод этой программы:

my_cos(M_PI * 1 / 3) = 0.5
my_cos(M_PI * 2 / 3) = -0.499567
my_cos(M_PI) = -0.976022
my_cos(0) = 1
my_cos(2 * M_PI) = 1

Как вы можете видеть, наша функция подсчитывает косинус угла с погрешностью.

Функции cosl и cosf

Функции cosl и cosf работают как и обычный cos, только с другими типами. Давайте посмотрим на прототип функции cosl:

long double cosl (long double x);

Как можете видеть, функция cosl принимает и возвращает long double (cos принимает и возвращает просто double). Теперь давайте посмотрим на cosf:

float cosf (float x);

Тут мы уже видим float. Давайте попробуем сравнить результаты этих функций:

cout << "cosf(M_PI * 1 / 2) = " << cosf(M_PI * 1 / 2) << endl;
cout << "cos (M_PI * 1 / 2) = " << cos(M_PI * 1 / 2) << endl;
cout << "cosl(M_PI * 1 / 2) = " << cosl(M_PI * 1 / 2) << endl;

Вывод программы:

cosf(M_PI * 1 / 2) = -4.37114e-08
cos (M_PI * 1 / 2) = 6.12323e-17
cosl(M_PI * 1 / 2) = 6.12323e-17

Все результаты близки к нулю, но немного отличаются. Это из-за разной точности типов данных, которыми они оперируют.

Интересное
Последние новости в мире программирования
Самые свежие новости и полезные материалы в моем telegram канале.
go

Упражнения

  1. Использование cos:
    Напишите программу на C++, которая запрашивает у пользователя угол в радианах, вычисляет его косинус с помощью функции cos и выводит результат. Также программа должна выводить введенный пользователем угол.

  2. Собственная реализация cos:
    Используя ряд Тейлора из статьи, создайте свою функцию для вычисления косинуса. Проверьте её работу на различных углах и сравните с результатами стандартной функции cos.

  3. Сравнение точности:
    Напишите программу, которая сравнивает результаты вычисления косинуса с использованием стандартной функции cos и вашей собственной реализации. Выведите разницу между ними для различных углов.

Если хотите всегда быть в курсе последних новостей в мире программирования и IT, подписываетесь на мой Telegram-канал, где я делюсь свежими статьями, новостями и полезными советами. Буду рад видеть вас среди подписчиков!

log в C++
В этом уроке вы познакомитесь с функцией log в C++. Данная функция позволяет нам получить натуральный логарифм числа. Мы разберемся с тем как работает функция log в теории и закрепим изученное на практике.
go
Функция find в C++
Разберемся в функции find из C++ и научимся использовать ее с такими контейнерами, как vector и set.
go
Функция atoi в C++
Функция atoi позволяет получить число из строки. В данной статье вы узнаете, как использовать данную функцию, возможные проблемы, а также реализуете аналог данной функции сами. Закрепить изученный материал нам помогут упражнения в конце статьи.
go
strcat в C/C++
Функция strcat используется в языках C и C++ для соединения (конкатенации) строк. В статье будут разобраны примеры использования этой функции. Также в конце статьи есть упражнения.
go
Map в C++
В данном уроке вы узнаете: что такое map, как правильно его использовать, какими функциями можно оперировать, а также стоит ли его использовать у себя в проектах.
go
strlen в C/C++
Функция strlen используется в языке программирования C для подсчета количества символов в строке. В статье будут разобраны примеры использования этой функции. Также мы реализуем эту функцию сами, а в конце статьи есть упражнения для закрепления материала.
go
Функция rand в C++
Язык C++ имеет несколько способов генерации случайных чисел. Функция rand - один из самых популярных способов получить случайное число. В этой статье мы научимся использовать эту функцию, генерировать случайные числа в диапазоне, а также реализуем свой простенький генератор случайных чисел.
go
vector::size в C++
В C++, контейнер std::vector представляет собой динамический массив, который может автоматически изменять свой размер. Часто возникает необходимость определить, сколько элементов на данный момент содержит vector. Встречайте функцию size! В этой статье мы рассмотрим, как работает функция size, покажем практические примеры и расскажем о других полезных функциях.
go
map::count в C++
C++ предлагает множество функций для работы с контейнерами. Одна из таких функций, count, позволяет узнать, существует ли ключ в std::map. В этой статье вы узнаете, когда она может вам пригодится.
go

Обсуждение

Содержание
Подпишись на мой Telegram-канал
Получай последние новости о технологиях и программировании!