Бинарный поиск в C++: подробное руководство

Всем привет! В прошлом уроке мы изучили, как найти определенный ключ в массиве с помощью простого алгоритма - линейного поиска. Также в том уроке мы упомянули, что последовательный поиск это не единственный в своем роде алгоритм для поиска элемента. Один из таких алгоритмов - бинарный поиск. Также его еще называют двоичный поиск.

Сегодня мы и изучим его. Также попытаемся ответить на такие вопросы: как бинарный поиск работает в программе, плюсы и минусы его использования у себя в коде и в каких структурах данных можно его применять, а в каких нет. Поехали!

Интересное

Последние новости в мире программирования

Самые свежие новости и полезные материалы в моем telegram канале.

Что такое бинарный поиск

Линейный поиск по сравнению с бинарным - дешевая подделка. Бинарный поиск - очень быстрый алгоритм с не сложной реализацией, который находит элемент с определенным значением в уже отсортированном массиве.

Очень важно помнить! Алгоритм будет работать правильно, только с отсортированным массивом. А если по случайности вы забыли отсортировать массив перед его использованием, то в большинстве случаев тот ответ, который подсчитал алгоритм, будет неверным.

Принцип работы бинарного поиска

Давайте рассмотрим задачку, чтобы понять как работает алгоритм. Охранной службе морского флота поступило сообщение о том, что некто пытается пронести на корабль бомбу. Диверсант пока находится у причала. Допустим, что в нашем распоряжении имеется прибор, который может определить, есть ли бомба в комнате. Необходимо как можно быстрее определить, у кого находится бомба.

Самым легким и самым долгим по времени решением, будет поочередная проверка пассажиров в комнате с прибором (это линейный поиск). Но это слишком долго.

Давайте сделаем по-другому. Поделим пополам всех пассажиров и разведем их по двум комнатам. Так с помощью прибора мы сможем узнать, в какой из двух комнат находится бомба. В итоге такого маневра мы уменьшим число подозреваемых в два раза. С остальным числом подозреваемых сделаем также: разделим их на две группы и разместим в разных комнатах. Так продолжаем, пока не узнаем кто диверсант.

В задаче выше охранники использовали алгоритм двоичного поиска для нахождения диверсанта. В обычной программе принцип работы бинарного поиска такой же, как и в примере, выше.

Как создать бинарный поиск в C++

Давайте посмотрим как работает бинарный поиск на примере.В примере ниже в строке 9 мы создали массив arr на 10 элементов и в строке 12 предложили пользователю с клавиатуры заполнить его ячейки.

В строке 20 мы предлагаем пользователю ввести ключ (который нужно будет найти в массиве), а дальше мы с бинарным поиском проверим массив на наличие введенного ключа пользователем. Если мы найдем ключ в массиве, то выведем индекс ячейки, в которой находится ключ.

#include <iostream>
#include <algorithm>

using namespace std;

int main() {
  setlocale(LC_ALL, "rus");

  int arr[10]; // создали массив на 10 элементов
  int key; // создали переменную в которой будет находиться ключ

  cout << "Введите 10 чисел для заполнения массива: " << endl;
 
  for (int i = 0; i < 10; i++) {
    cin >> arr[i]; // считываем элементы массива
  }

  sort (arr, arr + 10); // сортируем с помощью функции sort (быстрая сортировка)

  cout << endl << "Введите ключ: ";

  cin >> key; // считываем ключ

  bool flag = false;
  int l = 0; // левая граница
  int r = 9; // правая граница
  int mid;

  while ((l <= r) && (flag != true)) {
    mid = (l + r) / 2; // считываем срединный индекс отрезка [l,r]

    if (arr[mid] == key) flag = true; //проверяем ключ со серединным элементом
    if (arr[mid] > key) r = mid - 1; // проверяем, какую часть нужно отбросить
    else l = mid + 1;
  }

  if (flag) cout << "Индекс элемента " << key << " в массиве равен: " << mid;
  else cout << "Извините, но такого элемента в массиве нет";
  
  system("pause");
  return 0;
}

Бинарный поиск находится в строках 29 - 35. В строке 27 мы создали переменную mid, в которой будет храниться индекс среднего элемента (из отрезка [l, r]). В строке 27 считываем средний элемент отрезка [l, r] в переменную mid, по формуле: (l + r) / 2 (в которой l - левая граница, r - правая граница). В строке 29 проверяем условие arr[mid] == key:

• Если результат условия равен true, то булевой переменной flag присваиваем значение true (это значит, что мы нашли ключ).

В строке 30 мы проверяем условие arr[mid] > key:

• Если значение arr[mid] больше ключа, то переменной r присваиваем значение mid. Потому что проверять верхнюю часть не имеет смысла, так как ключ может находится только в ячейках ниже индекса mid (это если массив отсортирован по возрастанию).
• Если значение arr[mid] меньше ключа, то переменной l присваиваем значение mid. Потому что проверять нижнюю часть не имеет смысла, так как ключ может находится только в ячейках выше индекса mid (это если массив отсортирован по возрастанию).

В строке 37 мы проверяем flag:

• Если flag равен true, значит мы нашли ключ, а значит выводим “Индекс элемента key в массиве равен mid“.
• Если flag равен false, то выводим “Извините, но такого элемента в массиве нет”.

Давайте выполним этот код:

Напишите 10 чисел для заполнения массива:
17 20 26 31 44 54 55 65 77 93

Введите ключ : 54
Индекс элемента 54 в массиве равен: 5
Process returned 0 (0x0) execution time : 0.005 s
Press any key to continue.

А если такого ключа нет в массиве :

Напишите 10 чисел для заполнения массива:
17 20 26 31 44 54 55 65 77 93

Введите ключ : 18
Извините, но такого элемента в массиве нет
Process returned 0 (0x0) execution time : 0.005 s
Press any key to continue.

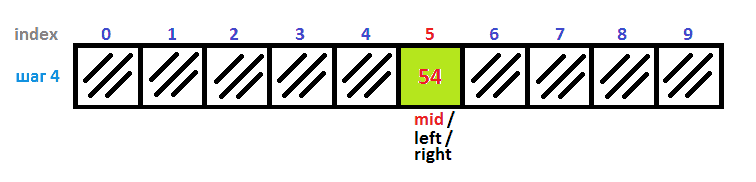
На картинке ниже находится отсортированный массив arr с примера выше.

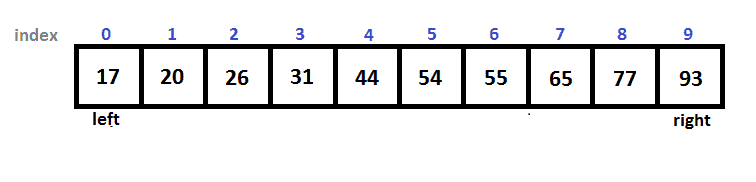
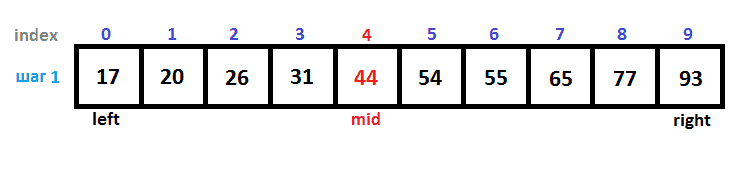
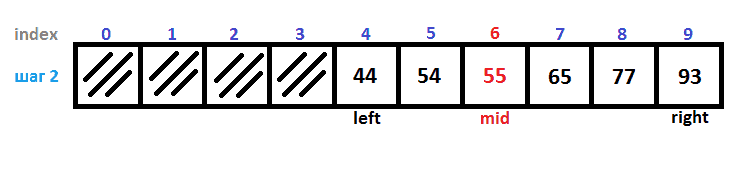
Дальше на рисунках вы можете увидеть, как двоичный поиск за четыре итерации нашел ключ 54:

Интересное

Последние новости в мире программирования

Самые свежие новости и полезные материалы в моем telegram канале.

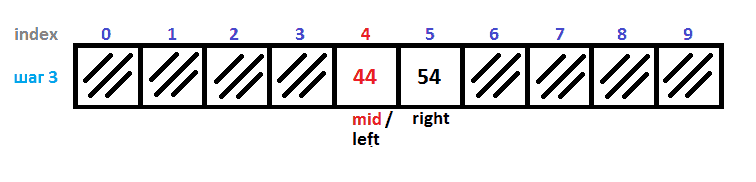
Как можно улучшить бинарный поиск

Бинарный поиск можно оптимизировать, как и все другие алгоритмы. Для его оптимизации можно уменьшить условие цикла ПОКА(while):

int l = 0;
int r = n; // в этом случае присваивается именно n
int mid;

while (l < r) {
    mid = (l + r) / 2; // считываем срединный индекс отрезка [l,r]

    if (arr[mid] > key) r = mid; // проверяем, какую часть нужно отбросить с поиска
    else l = mid + 1;
}

r--; // уменьшаем на один 

if (arr[r] == key) cout << "Индекс элемента " << key << " в массиве равен: " << r; 
else cout << "Извините, но такого элемента в массиве нет";

В этом случае изначально r нам нужно присвоить значение n, а не n - 1 как обычно. После выполнения, в переменной r - 1 будет храниться номер элемента, равного key, если такой элемент конечно есть в массиве. В ином случае, если элемента нет, то r будет место в массиве, куда можно вставить переменную key и не нарушить упорядоченность массива (такой принцип используются в сортировке бинарными вставками).

В строке 12 заранее уменьшаем r на один.

Плюсы и минусы использования бинарного поиска

Плюсы:

1. Реализация алгоритма достаточна легкая;
2. Быстрая работа алгоритма;

Минусы:

1. Для поиска массив должен быть упорядочен(отсортирован);
2. Двоичный поиск должен иметь возможность обратится к любому элементу данных (по индексу). А это значит, что все структуры данных, которые построены на связных списках использоваться не могут;

Мы советуем вам всегда использовать бинарный поиск при работе с массивами или векторами. Обычно прогеры применяют бинарный поиск с помощью функций.

Закрепление бинарного поиска

Для закрепления материала объявите массив на 10 элементов, предложите пользователю заполнить массив и ввести ключ. Используя бинарный поиск найдите ключ в массиве. Надеемся, что эта статья помогла вам узнать, что такое бинарный поиск и как он работает. Если вы нашли ошибки в статье или хотите задать вопрос, то пишите в комментарии. Удачи!

« Пузырьковая сортировка в C++

Линейный поиск в C++ »